研究紹介

レート歪み理論:
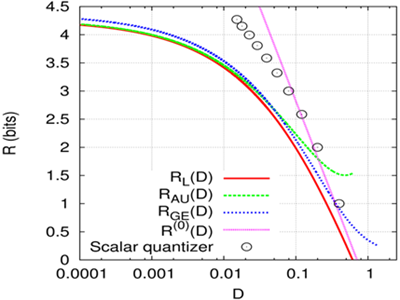　歪み有りデータ圧縮は、データを圧縮する際、ある程度の歪みを許す（データを壊してしまってもよい）状況を扱い、画像や音声データなどの圧縮に用いられています。一般に、歪みの度合いが大きくても良ければ、その分圧縮することができるため、歪みの量の増加とともに、符号長（1入力あたりの符号長になおしたものはレートと呼ばれます）が減少する曲線を描くことができます。実際の符号化法で実現できる符号長には限界があることが知られており、歪み量の関数としてレート歪み関数（曲線）と呼ばれます。これはデータの生成過程（情報源）と歪みを測る尺度について固有な関数ですが、わずかな例でしか明らかにされておらず、圧縮限界にせまる方法も明らかにされていません。
　この研究では、クラスタリング（データを自動的にグループ分けする）手法やベイズ推論における事前分布の最適化法に対し、レートと歪みのトレードオフを求める問題としての解釈を与え、複雑な歪み尺度を用いた学習法に対して、その性能の限界を示すレート歪み関数の評価を行っています。

ベイズ推論とMDL原理:
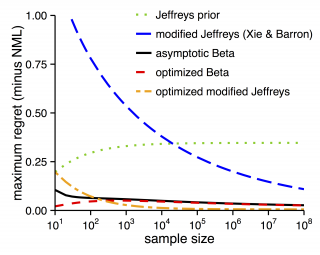　データ系列を短く圧縮しても完全に再現できるように符号化する方法はコンピュータ上のファイル圧縮やデジタル通信に広く用いられています。このときどんな系列が与えられてもそれなりに短く圧縮することを考えるアプローチはユニバーサル符号化と呼ばれます。符号の短さは系列の各記号を精度良く予測することと対応するため、予測に用いている学習モデルの良さと考えることができ、学習モデルの選択規準としてMDL (Minimum Description Length)規準と呼ばれています。しかしながら、最良予測法は系列の長さnに依存し、その計算にはnが大きくなると膨大な計算量が必要になります。
　この研究では、予測法を系列長nに応じて設計するかどうかと、最良予測法を精度良く近似することとの関係を明らかにし、ベイズ推論による効率的な予測法を導出しています。

データ可視化:
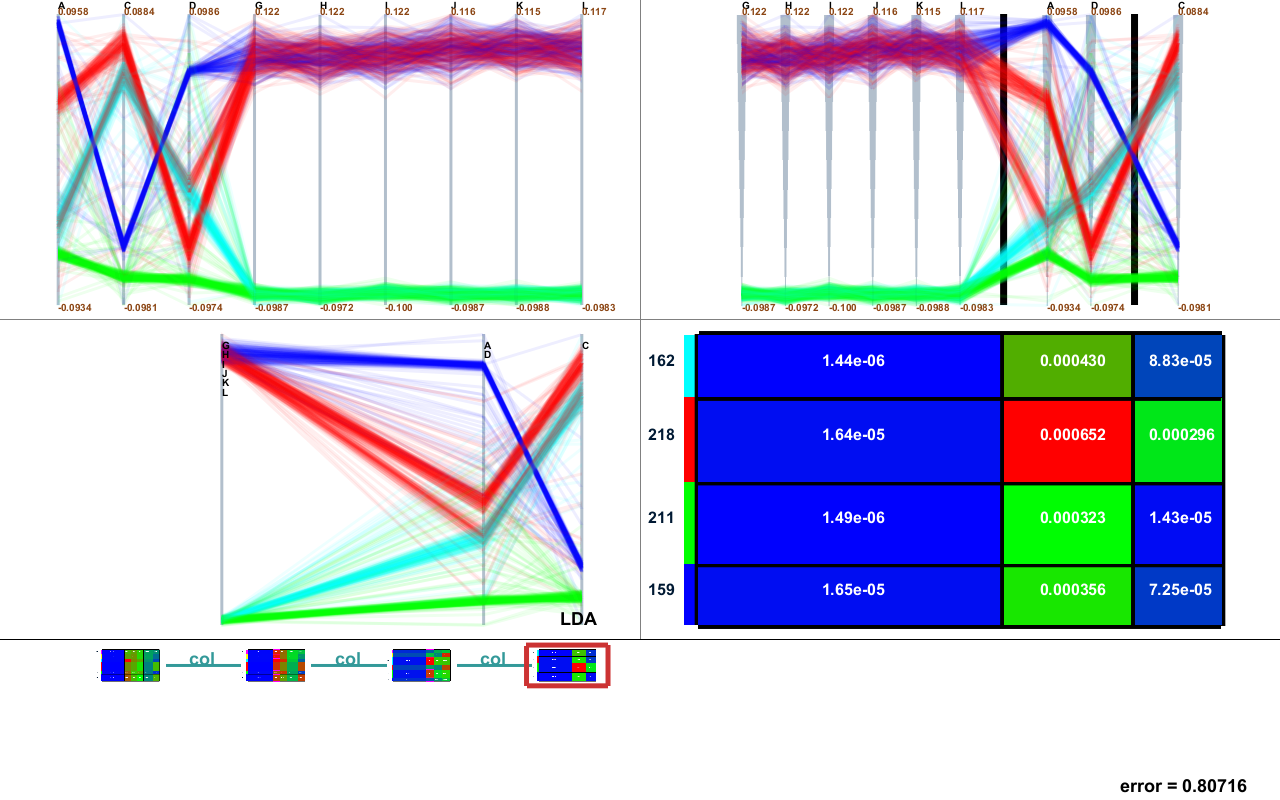　多変量データの解析においては、平行に並べた軸上での各変量の値を結ぶ折れ線によりデータを表す平行座標系表示などを用いることによりデータの全体像を可視化することができます。しかしながら、折れ線が複雑に込み入りデータの構造が見えにくくなってしまったり、軸の配置によっては変量同士の関係が抽出しづらくなってしまいます。
　この研究ではデータサンプルと変量のクラスタリング（グループ分け）を同時に行うバイクラスタリング手法を拡張し、データサンプルのクラスタ構造や変量間の関係を抽出、可視化するインタラクティブなデータ解析法を提案しています。

教員紹介ページ

▲ページトップに戻る